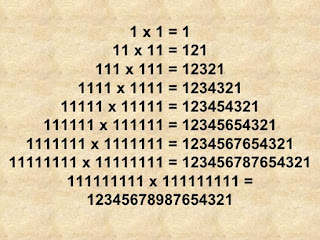mathematics calculation

Me doing mathematics

Math talk

Improving mathematics

Mathematics in real life

1. Math Helps You Build Things

Ask any contractor or construction worker--they'll tell you just how important math is when it comes to building anything.

To create something of lasting value out of raw materials requires creativity, the right set of tools, and a broad range of mathematics.

Figuring the total amount of concrete needed for a slab; accurately measuring lengths, widths, and angles; and estimating project costs are just a few of the many cases in which math is necessary for real-life home improvement projects.

Whether students work in construction jobs in the future or own a home, having the ability to do minor home improvements will save a lot of money and provide a sense of accomplishment and self-reliance. 

Teacher Tip: Consider incorporating a small building project in the classroom--like a simple house out of cardboard boxes or a small wooden boat from a kit--to reteach math-related skills such as measuring, estimating, angles, and following instructions.

2. Math is in the Grocery Store

One of the more obvious places to find people using math in everyday life is at your neighborhood grocery store.

Grocery shopping requires a broad range of math knowledge from multiplication to estimation and percentages.

Each time you calculate the price per unit, weigh produce, figure percentage discounts, and estimate the final price, you're using math in your shopping experience.

Teacher Tip #1: Encourage students to play math challenges at the grocery store with their family. For example, they can estimate the total cost of all groceries prior to checkout. For a greater challenge, encourage students to incorporate coupons, sales, and adjusted pricing for bulk items.

Your little bargain shoppers will thank you later when they’re saving money on their own groceries.

Teacher Tip #2: You could also organize a field trip to the grocery store--with the help of a few parents working with smaller student groups--making lists and pricing out items ahead of time, that your class can then use to cook with (see below)!

5. Math Helps You Save Money

Most experts agree that without strong math skills, people tend to invest, save, or spend money based on their emotions.

Here's the kicker:

To add to this dilemma, those individuals with poor math fundamentals typically make greater financial mistakes like underestimating how quickly interest accumulates.

A student who thoroughly grasps the concepts of exponential growth and compound interest will be more inclined to better manage debt.

Financial knowledge decays over time, so it’s important to keep young people involved.

By continually showing how specific math lessons apply to real life financial situations and budgeting, kids can learn how to properly spend and save their money without fear or frustration.

Teacher tip: Practice investing! Allot your students a set amount of pretend money individually or in groups. After teaching them about saving, investing, and interest, have them make financial decisions with their cash. Follow the stock market and check in on their savings weekly so they can see their totals rise or fall.

6. Math Lets You Manage Time

Time is our most valuable asset.

Teach your students about the value of time by not only teaching how to tell time on analogue and digital clocks, but about the world clock, time zones, calendars, and the value of how they spend their precious time.

In our fast-paced, modern world, we can easily get distracted and find the time has blown by without accomplishing what we meant to.

Teacher tip: Have your students set goals and determine how much time they must put aside daily or weekly to achieve these goals. Have your students calendar their time, create their own to-do lists, and give their tasks a number to rank what their priorities are. Not only are you teaching math, but you're helping a child learn how to organize their life and achieve their dreams!

The bottom line is:

Math is everywhere, operating in real life ways all around us.

So, the next time you or one of your students says, "I'm never going to use this math again!" remember the above examples, to help them be motivated to keep learning math!

2019 year calculation

Mathematics shapes

euclidian number

bees can do arithmetic

Researchers set out to test whether bees could do math, building on a groundbreaking finding that bees understand the concept of zero. The new study shows bees can be taught to recognize colors as symbolic representations for addition and subtraction, and use this information to solve arithmetic problems. The revelation that even the miniature brain of a honeybee can grasp basic mathematical operations has implications for the future development of AI.
Researchers have found bees can do basic mathematics, in a discovery that expands our understanding of the relationship between brain size and brain power.

Building on their finding that honeybees can understand the concept of zero, Australian and French researchers set out to test whether bees could perform arithmetic operations like addition and subtraction.

Solving maths problems requires a sophisticated level of cognition, involving the complex mental management of numbers, long-term rules and short term working memory.

The revelation that even the miniature brain of a honeybee can grasp basic mathematical operations has implications for the future development of Artificial Intelligence, particularly in improving rapid learning.

Led by researchers from RMIT University in Melbourne, Australia, the new study showed bees can be taught to recognise colours as symbolic representations for addition and subtraction, and that they can use this information to solve arithmetic problems.

RMIT's Associate Professor Adrian Dyer said numerical operations like addition and subtraction are complex because they require two levels of processing.

"You need to be able to hold the rules around adding and subtracting in your long-term memory, while mentally manipulating a set of given numbers in your short-term memory," Dyer said.

"On top of this, our bees also used their short-term memories to solve arithmetic problems, as they learned to recognise plus or minus as abstract concepts rather than being given visual aids.

"Our findings suggest that advanced numerical cognition may be found much more widely in nature among non-human animals than previously suspected.

"If maths doesn't require a massive brain, there might also be new ways for us to incorporate interactions of both long-term rules and working memory into designs to improve rapid AI learning of new problems."

There is considerable debate around whether animals know or can learn complex number skills.

Many species can understand the difference between quantities and use this to forage, make decisions and solve problems. But numerical cognition, such as exact number and arithmetic operations, requires a more sophisticated level of processing.

Previous studies have shown some primates, birds, babies and even spiders can add and/or subtract. The new research, published in Science Advances, adds bees to that list.

A school for bees? How the honeybees were trained

The experiment, conducted by PhD researcher Scarlett Howard in the Bio Inspired Digital Sensing-Lab (BIDS-Lab) at RMIT, involved training individual honeybees to visit a Y-shaped maze.

The bees received a reward of sugar water when they made a correct choice in the maze, and received a bitter-tasting quinine solution if the choice was incorrect.

Honeybees will go back to a place if the location provides a good source of food, so the bees returned repeatedly to the experimental set-up to collect nutrition and continue learning.

When a bee flew into the entrance of the maze they would see a set of elements, between 1 to 5 shapes.

The shapes were either blue, which meant the bee had to add, or yellow, which meant the bee had to subtract.

After viewing the initial number, the bee would fly through a hole into a decision chamber where it could choose to fly to the left or right side of the maze.

One side had an incorrect solution to the problem and the other side had the correct solution of either plus or minus one. The correct answer was changed randomly throughout the experiment to avoid bees learning to visit just one side of the maze.

At the beginning of the experiment, bees made random choices until they could work out how to solve the problem. Eventually, over 100 learning trials that took 4 to 7 hours, bees learned that blue meant +1, while yellow meant -1. The bees could then apply the rules to new numbers.

Scarlett Howard said the ability to do basic maths has been vital in the flourishing of human societies historically, with evidence that the Egyptians and Babylonians used arithmetic around 2000BC.

"These days, we learn as children that a plus symbol means you need to add two or more quantities, while a minus symbol means you subtract," she said.

"Our findings show that the complex understanding of maths symbols as a language is something that many brains can probably achieve, and helps explain how many human cultures independently developed numeracy skills."

bramagupta teaching

                                                        bramagupta teaching: 

Arithmetic

In Brahmasphutasiddhanta, Multiplication was named Gomutrika. He explained how to find the cube and cube-root of an integer and gave rules facilitating the computation of squares and square roots.

He also gave rules for dealing with five types of combinations of fractions –  a/c + b/c; a/c × b/d; a/1 + b/d; a/c + b/d × a/c = a(d + b)/cd; and a/c − b/d × a/c = a(d − b)/cd .

He gave the sum of the squares of the first n natural numbers as n(n + 1)(2n + 1)⁄ 6 and the sum of the cubes of the first n natural numbers as (n(n + 1)⁄2)².

Zero

The most notable innovations that Brahmagupta is remembered for is his look and pursuit of the number zero. Until this time, the zero had not been thought of as a number. He formulated equations that allowed zero to be used in positives and negatives. Although he did not use those specific words, Brahmagupta did follow with the importance in the need of the zero placement. Without the use of zero and its value defined, according to him, arithmetic really had nowhere to go.

Brahmagupta describes operations on negative numbers. He first describes addition and subtraction,

The sum of two positives is positives, and sum of two negatives negative; of a positive and a negative [the sum] is their difference; if they are equal it is zero. The sum of a negative and zero is negative, [that] of a positive and zero positive, [and that] of two zeros zero.

A negative minus zero is negative, a positive [minus zero] positive; zero [minus zero] is zero. When a positive is to be subtracted from a negative or a negative from a positive, then it is to be added.

Brahmagupta’s Look at Zero listed:

• Zero minus zero is a zero.
• The product of zero multiplied by zero is zero.
• A debt minus zero is a debt.
• A fortune minus zero is a fortune.
• A debt subtracted from zero is a fortune.
• fortune subtracted from zero is a debt.
• The product of zero multiplied by a debt or fortune is zero.

Brahmagupta states that 0/0 = 0 and as for the question of a/0 where a ≠ 0 he did not commit himself. His rules for arithmetic on negative numbers and zero are quite close to the modern understanding, except that in modern mathematics division by zero is left undefined.

2019 calculation

multiplication facts

Dice Games to Teach Multiplication Facts

dice image by Olga Shelego from Fotolia.com

Capturing and holding the attention of students can be challenging in any content area, and math is definitely one of those areas. By using games in math, the interest of the student will be held, and while the student is playing the game, he is learning. Using dice to teach multiplication facts provides an excellent opportunity for the students to learn multiplication through a game. Once the game is learned at school, the students can play the game at home with siblings or parents and the only items needed are inexpensive dice.

Single Digit Multiplication

Students roll one die to see who goes first. The student who rolls the highest number goes first. The student rolls two dice and multiplies the numbers. That student writes down the problem and the answer. The partner checks the problem. If the answer is correct, the student who rolled the dice receives a tally mark. The students then switch roles. The first student to the predetermined amount of tally marks is the winner.

Double Digit Multiplication

Students role two dice to see who goes first. The numbers on the dice are multiplied and the highest answer goes first. Counters are used to determine the winner. Counters can be pennies, beans or other small objects. To add more excitement, use small pieces of candy as counters. The first student roles three dice one at a time. The first two dice are the "to" number for the multiplication problem. For example, if a three and a two are rolled, the number will be 32. The third dice is rolled to provide the single digit number to multiply the double digit number by. The student solves the problem on paper and another student checks her work. If the student is correct, a counter is given to that student. If the student is not correct, a counter is given to the other student. The student with the most counters after a preset time or number of problems is the winner.

maths in nature

                                            maths in nature:
The concept of ‘Math in Nature’ is as innate as a person taking their first breath. Most would agree that our conception of math in its basic form has been derived as a means to describe aspects of our environment as an element of a much larger sociological agreement. So to say that “math exists in nature” is as redundant a statement as saying that humans themselves exist in nature. However in researching this topic one can not help but marvel at how well ‘mathematics’ corresponds with the grand scheme of things and ultimately makes one wonder what came first; an issue of the chicken or the egg as it were. 
Whatever the case, we can rationalize that math in nature is factual in its tangibility. It is this outstanding quality that makes the use of math in nature a tremendous resource for the classroom. Too often we force mathematical concepts on the basis of blind faith, while examples such as these are quite literally all around us. Demonstrating math in nature is an ideal approach for illustrating what many students will regard as arbitrary information and should be utilized by all teachers as a tool to increase learner interest

mathematical symbols