The Epidemiological Parameter R0
![[IMAGE: measles]](https://plus.maths.org/issue14/features/diseases/measles.gif)
Measles: A histologic section of the lung of a child (autopsy). Hyaline membranes are present, preventing alveolar oxygen exchange resulting in respiratory failure.
Many interesting and useful results have been proved for the simple SIR model, but before we can explore this rich subject area, we need a further bit of Epidemiological notation. One fundamental parameter governs the spread of diseases, and is also related to the long term behaviour and the level of vaccination necessary for eradication. This parameter is called the basic reproductive ratio, 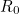 .
. 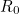 is defined by epidemiologists as "the average number of secondary cases caused by an infectious individual in a totally susceptible population". As such
is defined by epidemiologists as "the average number of secondary cases caused by an infectious individual in a totally susceptible population". As such 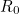 tells us about the initial rate of increase of the disease over a generation. When
tells us about the initial rate of increase of the disease over a generation. When 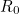 is greater than 1, the disease can enter a totally susceptible population and the number of cases will increase, whereas when
is greater than 1, the disease can enter a totally susceptible population and the number of cases will increase, whereas when 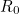 is less than 1, the disease will always fail to spread. Therefore, in its simplest form
is less than 1, the disease will always fail to spread. Therefore, in its simplest form 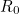 tells us whether a population is at risk from a given disease.
tells us whether a population is at risk from a given disease.
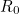 .
. 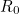 is defined by epidemiologists as "the average number of secondary cases caused by an infectious individual in a totally susceptible population". As such
is defined by epidemiologists as "the average number of secondary cases caused by an infectious individual in a totally susceptible population". As such 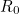 tells us about the initial rate of increase of the disease over a generation. When
tells us about the initial rate of increase of the disease over a generation. When 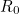 is greater than 1, the disease can enter a totally susceptible population and the number of cases will increase, whereas when
is greater than 1, the disease can enter a totally susceptible population and the number of cases will increase, whereas when 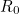 is less than 1, the disease will always fail to spread. Therefore, in its simplest form
is less than 1, the disease will always fail to spread. Therefore, in its simplest form 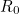 tells us whether a population is at risk from a given disease.
tells us whether a population is at risk from a given disease.| The value of R0 for some well-known diseases | |
|---|---|
| Disease | R0 |
| AIDS | 2 to 5 |
| Smallpox | 3 to 5 |
| Measles | 16 to 18 |
| Malaria | > 100 |
![[IMAGE: graphs for measles and plague]](https://plus.maths.org/issue14/features/diseases/comparison.gif)
The fit between cases and the SIR epidemic for bubonic plague and measles
A second use for 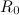 is looking at the behaviour of a single epidemic outbreak. Consider the situation when a new strain of influenza enters a totally susceptible population. Simple intuition tells us that the disease will spread rapidly through the population, infecting a large proportion of the population in a very short time. It is therefore plausible to ignore births and deaths in the population and solely concentrate on the disease dynamics. For these short-term epidemics, initially the number of cases increases exponentially (
is looking at the behaviour of a single epidemic outbreak. Consider the situation when a new strain of influenza enters a totally susceptible population. Simple intuition tells us that the disease will spread rapidly through the population, infecting a large proportion of the population in a very short time. It is therefore plausible to ignore births and deaths in the population and solely concentrate on the disease dynamics. For these short-term epidemics, initially the number of cases increases exponentially (![$I(t) \propto \exp [(R_0-1)t]$](https://plus.maths.org/MI/90b9df392b48306f801888b0f81bf872/images/img-0002.png) ). However, as more of the population enters the recovered class and there are fewer susceptibles, the disease spreads less well and eventually the number of cases declines. Due to this decline not everyone will be infected before the disease dies out. By looking at the long-term behaviour of the SIR model, Kermack and McKendrick were able to predict the proportion of individuals (
). However, as more of the population enters the recovered class and there are fewer susceptibles, the disease spreads less well and eventually the number of cases declines. Due to this decline not everyone will be infected before the disease dies out. By looking at the long-term behaviour of the SIR model, Kermack and McKendrick were able to predict the proportion of individuals (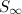 ) who would escape the infection,
) who would escape the infection,
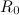 is looking at the behaviour of a single epidemic outbreak. Consider the situation when a new strain of influenza enters a totally susceptible population. Simple intuition tells us that the disease will spread rapidly through the population, infecting a large proportion of the population in a very short time. It is therefore plausible to ignore births and deaths in the population and solely concentrate on the disease dynamics. For these short-term epidemics, initially the number of cases increases exponentially (
is looking at the behaviour of a single epidemic outbreak. Consider the situation when a new strain of influenza enters a totally susceptible population. Simple intuition tells us that the disease will spread rapidly through the population, infecting a large proportion of the population in a very short time. It is therefore plausible to ignore births and deaths in the population and solely concentrate on the disease dynamics. For these short-term epidemics, initially the number of cases increases exponentially (![$I(t) \propto \exp [(R_0-1)t]$](https://plus.maths.org/MI/90b9df392b48306f801888b0f81bf872/images/img-0002.png) ). However, as more of the population enters the recovered class and there are fewer susceptibles, the disease spreads less well and eventually the number of cases declines. Due to this decline not everyone will be infected before the disease dies out. By looking at the long-term behaviour of the SIR model, Kermack and McKendrick were able to predict the proportion of individuals (
). However, as more of the population enters the recovered class and there are fewer susceptibles, the disease spreads less well and eventually the number of cases declines. Due to this decline not everyone will be infected before the disease dies out. By looking at the long-term behaviour of the SIR model, Kermack and McKendrick were able to predict the proportion of individuals (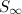 ) who would escape the infection,
) who would escape the infection,![\[ S_{\infty } = \exp ([1-S_{\infty }] R_0). \]](https://plus.maths.org/MI/90b9df392b48306f801888b0f81bf872/images/img-0004.png) |
![[IMAGE: graph of S_\infty]](https://plus.maths.org/issue14/features/diseases/Final_Size.gif)
A graphical method for calculating the percentage that escape infection
Although this expression cannot be evaluated analytically, by examining the two sides graphically (plotting 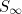 and
and ![$\exp ([1-S_{\infty }] R_0)$](https://plus.maths.org/MI/842c6bc099b915dafb1d50ca7b6df5a5/images/img-0002.png) on the same graph) it is clear that as
on the same graph) it is clear that as 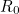 increases, fewer individuals escape the disease. Calculating
increases, fewer individuals escape the disease. Calculating 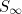 numerically, when
numerically, when 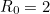 we find that
we find that 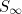 is approximately
is approximately 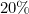 , whereas when
, whereas when 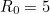 we get
we get 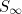 is approximately
is approximately 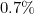 . Therefore, increasing
. Therefore, increasing 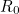 has a dramatic effect on the proportion that escape the outbreak.
has a dramatic effect on the proportion that escape the outbreak.
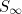 and
and ![$\exp ([1-S_{\infty }] R_0)$](https://plus.maths.org/MI/842c6bc099b915dafb1d50ca7b6df5a5/images/img-0002.png) on the same graph) it is clear that as
on the same graph) it is clear that as 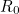 increases, fewer individuals escape the disease. Calculating
increases, fewer individuals escape the disease. Calculating 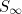 numerically, when
numerically, when 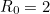 we find that
we find that 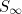 is approximately
is approximately 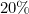 , whereas when
, whereas when 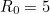 we get
we get 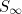 is approximately
is approximately 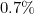 . Therefore, increasing
. Therefore, increasing 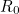 has a dramatic effect on the proportion that escape the outbreak.
has a dramatic effect on the proportion that escape the outbreak.
Finally, if we wish to model a disease that is endemic, that is, persists indefinitely in the population, our SIR model must also include births to replenish the level of susceptibles. In this case the long term behaviour of the disease can again be related to the parameter 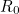 . The long-term proportion of susceptible individuals in the population, once the oscillations have died away, is given by
. The long-term proportion of susceptible individuals in the population, once the oscillations have died away, is given by
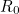 . The long-term proportion of susceptible individuals in the population, once the oscillations have died away, is given by
. The long-term proportion of susceptible individuals in the population, once the oscillations have died away, is given by![\[ S^{\star }= 1/R_0. \]](https://plus.maths.org/MI/842c6bc099b915dafb1d50ca7b6df5a5/images/img-0008.png) |
Therefore, those diseases that spread the most rapidly have the fewest susceptible individuals. (It is interesting to note that the long-term level of infection, 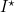 , does not depend on the parameter
, does not depend on the parameter 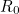 , but instead is dependent on the birth rate and the infectious period.)
, but instead is dependent on the birth rate and the infectious period.)
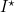 , does not depend on the parameter
, does not depend on the parameter 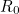 , but instead is dependent on the birth rate and the infectious period.)
, but instead is dependent on the birth rate and the infectious period.)
The concept behind vaccination is to reduce the proportion of susceptibles until the disease cannot survive. At the long-term level of susceptibles, 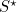 , each infectious individual on average causes one further secondary case. (If infectious individuals causes more or less than one case, then the level of infection would either rise or fall and the disease wouldn’t be stable.) Therefore, if we can reduce the number of susceptibles even further, so that the disease does less well, we can begin to eradicate the disease. The threshold level of vaccination (
, each infectious individual on average causes one further secondary case. (If infectious individuals causes more or less than one case, then the level of infection would either rise or fall and the disease wouldn’t be stable.) Therefore, if we can reduce the number of susceptibles even further, so that the disease does less well, we can begin to eradicate the disease. The threshold level of vaccination (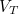 ) necessary to eradicate the disease is therefore
) necessary to eradicate the disease is therefore
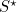 , each infectious individual on average causes one further secondary case. (If infectious individuals causes more or less than one case, then the level of infection would either rise or fall and the disease wouldn’t be stable.) Therefore, if we can reduce the number of susceptibles even further, so that the disease does less well, we can begin to eradicate the disease. The threshold level of vaccination (
, each infectious individual on average causes one further secondary case. (If infectious individuals causes more or less than one case, then the level of infection would either rise or fall and the disease wouldn’t be stable.) Therefore, if we can reduce the number of susceptibles even further, so that the disease does less well, we can begin to eradicate the disease. The threshold level of vaccination (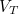 ) necessary to eradicate the disease is therefore
) necessary to eradicate the disease is therefore![\[ V_ T = 1- S^{\star } = 1 - 1/R_0. \]](https://plus.maths.org/MI/842c6bc099b915dafb1d50ca7b6df5a5/images/img-0012.png) |
It should now be clear why vaccination has allowed us to completely eradicate smallpox (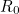 is approximately 4), whereas there are still cases of measles in Britain and the USA (
is approximately 4), whereas there are still cases of measles in Britain and the USA (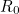 is approximately 17) despite mass vaccination, and why it is so very difficult to control malaria (
is approximately 17) despite mass vaccination, and why it is so very difficult to control malaria ( ). It is important to realize that we don’t need to vaccinate everybody to eradicate a disease; by a process known as herd immunity, for each person that is vaccinated the risk of infection for the rest of the community decreases. Therefore vaccination does not just protect the individual,
). It is important to realize that we don’t need to vaccinate everybody to eradicate a disease; by a process known as herd immunity, for each person that is vaccinated the risk of infection for the rest of the community decreases. Therefore vaccination does not just protect the individual,
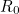 is approximately 4), whereas there are still cases of measles in Britain and the USA (
is approximately 4), whereas there are still cases of measles in Britain and the USA (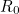 is approximately 17) despite mass vaccination, and why it is so very difficult to control malaria (
is approximately 17) despite mass vaccination, and why it is so very difficult to control malaria ( ). It is important to realize that we don’t need to vaccinate everybody to eradicate a disease; by a process known as herd immunity, for each person that is vaccinated the risk of infection for the rest of the community decreases. Therefore vaccination does not just protect the individual,
). It is important to realize that we don’t need to vaccinate everybody to eradicate a disease; by a process known as herd immunity, for each person that is vaccinated the risk of infection for the rest of the community decreases. Therefore vaccination does not just protect the individual,
No comments:
Post a Comment